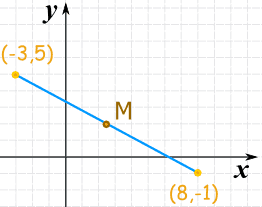
Tuesday, December 11, 2012
Thursday, November 1, 2012
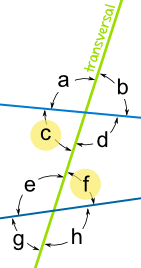
Same-Side Interior Angles
Created where a transversal crosses two (usually parallel) lines. Each pair of interior angles are inside the parallel lines, and on the same side of the transversal.
 |
| Example |
 |
| Real Example |
Right Triangle
A triangle where one of its interior angles is a right angle (90 degrees).
 |
| Example |
 |
| Real Example |
Corresponding Angles
two nonadjacent angles made by the crossing of two lines by athird line, one angle being interior, the other exterior, and bothbeing on the same side of the third line
Alternate Interior Angles
Same-Side Exterior Angles
Exterior Angles are created where a transversal crosses two (usually parallel) lines. Each pair of these angles are outside the parallel lines, and on the same side of the transversal.
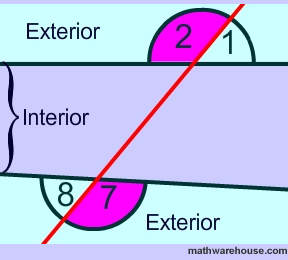 |
| Example |
 |
| Real example |
Friday, October 19, 2012
Tuesday, October 16, 2012
Obtuse Triangle
A triangle where one of the internal angles is obtuse (greater than 90 degrees).
 |
| Example |
 |
| Real life example |
Regular Polygon
A polygon that has all sides equal and all interior angles equal
 |
| Regular |
 |
| Real life example |
Altitude (of a triangle)
in the altitude of a triangle, the altitude refers to the perpendicular distance from the vertex to the opposide. In the image, note that the altitude is AD. AD is the altitude from A to BC.
Alternate Exterior Angles
Monday, October 1, 2012
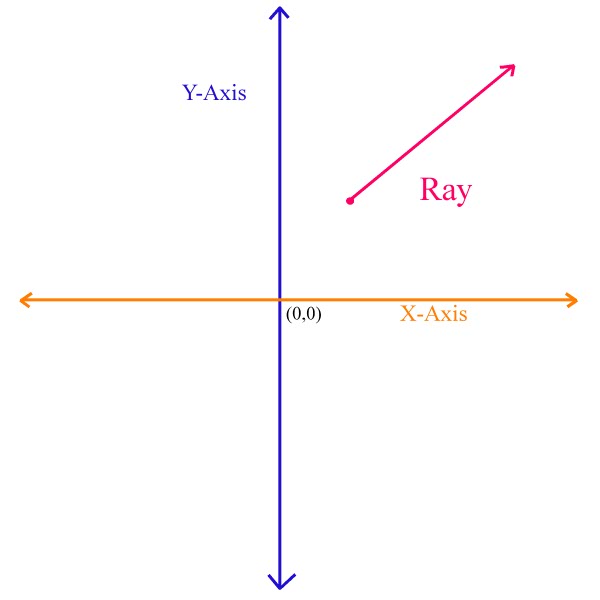
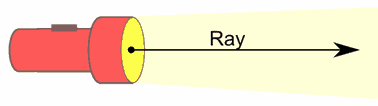
Ray
A line which starts at a point with given coordinates, and goes off in a particular direction to infinity, possibly through a second point.
Subscribe to:
Comments (Atom)